Lanjutan dari Panduan Lengkap Konsep Matematika (Part 1)
Konsep box model ini dapat digunakan secara luas baik oleh siswa/i Sekolah Dasar kelas 1 - 6. Untuk siswa/i kelas 6, Vyneapple lebih merekomendasikan mereka untuk mempelajari tentang metode aljabar. Box model berguna saat Anda melihat kata kunci "lebih dari","kurang dari" atau “memiliki A kali lebih banyak” pada soal cerita dengan bilangan pecahan.
Ikhwan memiliki 120 biskuit lebih banyak daripada Damar. Setelah Ikhwan memakan ⅙ dari jumlah biskuit miliknya dan Damar memakan ⅗ dari jumlah biskuit miliknya, Ikhwan memiliki 230 biskuit lebih banyak daripada Damar. Berapa jumlah biskuit Damar semula
Langkah 1: Gambarlah box model untuk jumlah biskuit Ikhwan dan Damar.

Langkah 2: Ubahlah nilai pecahan keduanya sehingga nilai penyebutnya sama.
1/6 x 5/5 = 5/30 artinya“Ikhwan makan 5 kotak dari 30 kotak miliknya.”
3/5 x 6/6 = 18/30 artinya “Damar makan 18 kotak dari 30 kotak miliknya.”
Langkah 3: Bagilah setiap kotak menjadi 30 kotak.
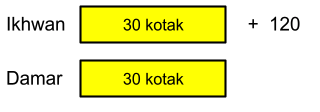
Langkah 4: Carilah bagian sisa dari 120.
⅚ x 120 = 100
Langkah 5: Gambarlah box model dari sisa.
Berdasarkan Langkah 2, maka sisa biskuit Ikhwan dan Damar adalah
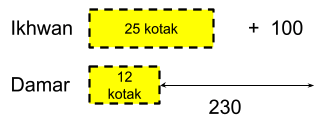
Langkah 6: Carilah nilai 1 kotak.
13 kotak = 230 - 100 = 130 1 kotak = 10
Langkah 7: Carilah nilai kotak Damar semula. 30 kotak = 30 x 10 = 300 (Jawaban)
Bagian yang tetap/ konstan maksudnya adalah salah satu bagian nilainya tetap sama sedangkan bagian yang lainnya berubah. Dalam hal ini, Anda perlu membuat bagian yang nilainya tetap sama tersebut dengan cara mengalikan atau membagi dengan bilangan lain.
Perbandingan jumlah gelang milik Jessica dan Nisa adalah 3 : 1. Setelah Nisa membeli 51 buah gelang lagi, perbandingan jumlah gelang Jessica dan Nisa menjadi 6 : 5. Berapa jumlah gelang Jessica dan Nisa semula?
Catatan: karena hanya Nisa yang membeli sejumlah gelang lagi, berarti jumlah gelang Jessica tetap sama.
Langkah 1: Buatlah rasio/ perbandingan dengan jumlah gelang Jessica tetap sama.
Sebelum
Jessica : Nisa = 3 : 1 = 6 : 2
Setelah
Jessica : Nisa = 6 : 5
Langkah 2: Carilah selisih sebelum dan setelah jumlah gelang Nisa.
5 - 2 = 3 satuan
Langkah 3: Carilah nilai 1 satuan.
3 satuan = 51
1 satuan = 51 ÷ 3 = 17
Langkah 4: Carilah jumlah gelang Jessica dan Nisa semula.
8 satuan = 8 x 17 = 136 (Jawaban)
Total yang tetap/konstan berarti jumlahnya tetap sama. Biasanya konsep ini menggunakan pertanyaan tentang "pemberian nilai (transfer internal)". Jika si A memberikan sejumlah nilai kepada si B, nilai A tentunya akan berkurang, sementara nilai B akan bertambah. Namun, ketika nilai keduanya dijumlahkan, maka total nilai keduanya (sebelum dan setelah) tetap sama banyak. Jadi, totalnya akan tetap sama.
Ayah memberikan uang saku dengan jumlah yang sama setiap bulan kepada Gina dan Jessica. Secara tidak sengaja, Jessica mendapat lebih banyak uang saku bulan ini. Perbandingan jumlah uang saku Gina dan Jessica adalah 5 : 8. Jessica memutuskan untuk memberikan sejumlah Rp 78.000 kepada Gina agar jumlah uang saku mereka sama banyak. Berapa banyak jumlah uang Gina di akhir?
Catatan: Setelah Jessica memberikan sejumlah uang kepada Gina, total uang keduanya tetap sama.
Langkah 1: Buatlah total uang saku Gina dan Jessica tetap sama untuk sebelum dan setelah.
Sebelum
Gina : Jessica : Total = 5 : 8 : 13
Setelah
Gina : Jessica : Total = 6,5 : 6,5 : 13
Langkah 2: Carilah selisih nilai perbandingan uang Jessica semula dan di akhir.
8 satuan - 6,5 satuan = 1,5 satuan
1,5 satuan = Rp 78.000
Langkah 3 : Carilah nilai 1 satuan.
1 satuan = Rp 78.000 ÷ 1,5 = Rp 52.000
Langkah 4: Carilah jumlah uang Gina di akhir.
6,5 satuan = Rp 52.000 x 6,5 = Rp 338.000 (Jawaban)
Selisih yang tetap/ konstan berarti selisihnya tetap sama. Biasanya konsep ini berlaku untuk pertanyaan yang berkaitan dengan "usia". Seiring berjalannya waktu, selisih usia antara 2 orang akan selalu sama, karena keduanya akan menjadi tua bersama.
12 tahun yang lalu, saat Andi merayakan ulang tahunnya, perbandingan umur Andi dan Adiknya adalah 7 : 5. Tahun ini, perbandingan umur Andi dengan Adiknya adalah 5 : 4. Berapa umur Andi sekarang?
Catatan: karena Andi dan adiknya tua bersama, maka selisih usia mereka pasti sama.
Langkah 1: Buatlah selisih usia Andi dan adiknya menjadi sama.
12 tahun lalu
Andi : Adik : Selisih = 7 : 5 : 2
Sekarang
Andi : Adik : Selisih = 5 : 4 : 1 = 10 : 8 : 2
Langkah 2: Carilah selisih perbandingan umur adik Andi 12 tahun lalu dan sekarang.
8 satuan - 5 satuan = 3 satuan
Langkah 3: Carilah nilai 1 satuan.
3 satuan = 12 tahun
1 satuan = 12 ÷ 3 = 4 tahun
Langkah 4: Carilah umur Andi sekarang.
10 satuan = 10 x 4 = 40 tahun (Jawaban)
Semua berubah maksudnya setiap bagiannya berubah, totalnya berubah dan selisihnya pun berubah. Tidak ada yang tetap sama.
Randy dan Boas telah menabung uang saat bulan puasa. Saat bulan puasa selesai, Randy menambah tabungannya Rp 250.000 dan Boas menambah Rp 80.000. Perbandingan uang yang ditabung Randy dan Boas saat bulan puasa adalah 5:7. Setelah bulan puasa, perbandingan uang mereka adalah 2:1. Berapa banyak tabungan Randy pada akhirnya?
Langkah 1: Tulislah perbandingan di awal dan perubahannya.

Langkah 2: Bandingkan nilai rasio setelah perubahan.
Catatan: karena Randy memiliki 2 kalinya dari Boas, maka kita harus mengalikan Boas dengan 2 agar nilainya sama dengan Randy.
1 x (5 satuan + Rp 250.000) = 2 x (7 satuan + Rp 80.000)
5 satuan + Rp 250.000 = 14 satuan + Rp 160.000
Langkah 3: Carilah nilai 1 satuan.
9 satuan = Rp 90.000
1 satuan = Rp 90.000 ÷ 9 = Rp 10.000
Langkah 4: Carilah tabungan Randy di akhir.
5 satuan + Rp 250.000 = 5 x Rp 10.000 + Rp 250.000 = Rp 300.000 (Jawaban)
Ini adalah tipe lain dari pertanyaan yang memberikan 2 kasus/kondisi. Kasus pertama menunjukkan kelebihan sementara kasus kedua menunjukkan kekurangan, bisa juga sebaliknya. Bisa juga kasus pertama dan kedua menunjukkan kelebihan, atau menunjukkan kekurangan.
Vira ingin memberikan balon kepada tamunya. Jika dia memberi mereka masing-masing 2 balon, dia akan memiliki 6 balon tersisa. Jika dia memberi mereka masing-masing 3 balon, dia akan kekurangan 9 balon.
a) Ada berapa tamu? ... tamu.
b) Berapa banyak balon yang dimiliki Vira? ... balon.
Langkah 1: Carilah selisih balon yang diberikan Vira.
3 - 2 = 1
Langkah 2: Carilah banyaknya tamu pada kasus 6 balon tersisa.
6 ÷ 1 = 6
Langkah 3: Carilah banyaknya tamu pada kasus 9 balon kurang.
9 ÷ 1 = 9
Langkah 4: Carilah jumlah tamu.
6 + 9 = 15 tamu (Jawaban a)
Langkah 5: Carilah jumlah balon.
15 x 2 + 6 = 36
atau
15 x 3 - 9 = 36 (Jawaban b)
Ketika Vira memasukkan sejumlah permen kacang ke dalam plastik yang berukuran 5, akan ada 2 permen kacang tersisa. Jika Vira memasukkan ke dalam plastik yang berukuran 7, akan ada 2 permen kacang tersisa. Berapa jumlah paling sedikit dari permen kacang tersebut?
Catatan: Anda tidak dapat menggunakan metode seperti yang sebelumnya, karena jumlah plastiknya berbeda pada kedua kasus.
Langkah 1: Sebutkan banyaknya permen kacang yang mungkin pada kasus 1.
7, 11, 15, 19, …
Langkah 2: Sebutkan banyaknya permen kacang yang mungkin pada kasus 2.
9, 15, 21, …
Langkah 3: Carilah nilai yang paling sedikit dan sama pada kedua kasus.
15 (Jawaban)
Yalma bekerja sebagai translator bahasa inggris. Ia diberikan tenggat waktu untuk menyelesaikan pekerjaannya. Jika Yalma menerjemahkan 60 halaman per hari, ia akan telat 5 hari dari tenggat waktu yang diberikan. Jika Yalma menerjemahkan 80 halaman per hari, ia dapat menerjemahkan 100 halaman lagi sebelum tenggat waktu habis. Berapa jumlah halaman yang harus diterjemahkan?
Langkah 1: Carilah selisih halaman.
80 - 60 = 20 halaman
Langkah 2: Tambahkan kelebihan dan kekurangan halaman dari tenggat waktu yang diberikan.
Pada kasus 1
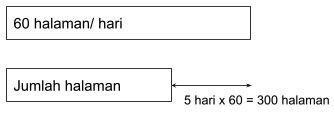
Pada kasus 2

5 hari x 60 halaman = 300 halaman
300 + 100 = 400 halaman
Langkah 3: Carilah tenggat waktu.
400 ÷ 20 = 20 hari
Langkah 4: Carilah total halaman yang harus dikerjakan.
20 x 60 + 300 = 1.500
atau
20 x 80 - 100 = 1.500 (Jawaban)
Sama seperti konsep sebelumnya, berikut adalah contoh soal cerita untuk mencari nilai sisa.
Damar memasukkan sejumlah coklat ke dalam 12 plastik sama banyak. 3 diantara plastik tersebut rusak, sehingga ia memindahkan coklat dari 3 plastik tersebut ke 9 plastik yang tersisa. Sehingga 9 plastik yang tersisa tersebut memiliki tambahan 10 coklat masing-masing. Berapa jumlah coklat seluruhnya?
Langkah 1: Carilah jumlah sisa coklat yang ditambahkan ke 9 plastik.
10 x 9 = 90
Langkah 2: Carilah jumlah coklat pada plastik yang rusak.
90 ÷ 3 = 30
Langkah 3: Carilah jumlah coklat keseluruhan.
30 × 12 = 360 coklat (Jawaban)
Mia dan Eli diberikan sejumlah uang yang sama banyak oleh Ibunya. Mia menghabiskan sejumlah Rp 60.000 per hari sementara Eli menghabiskan sejumlah Rp 75.000 per hari. Ketika sisa uang Mia Rp 200.000, sisa uang Eli adalah Rp 125.000. Berapa jumlah masing-masing uang yang Mia dan Eli semula?
Langkah 1: Carilah selisih uang yang dihabiskan Mia dan Eli per hari.
Rp 75.000 - 60.000 = Rp 15.000
Langkah 2: Carilah selisih sisa uang Mia dan Eli.
Rp 200.000 - Rp 125.000 = Rp 75.000
Langkah 3: Carilah total hari.
Rp 75.000 ÷ Rp 15.000 = 5 hari
Langkah 4: Carilah jumlah masing-masing uang semula.
5 x Rp 60.000 + Rp 200.000 = Rp 500.000
atau
5 x Rp 75.000 + Rp 125.000 = Rp 500.000 (Jawaban)
Masih ada beberapa konsep matematika lagi yang harus Anda pelajari. Semakin banyak konsep yang diketahui, maka semakin banyak cara yang dapat digunakan anak Anda untuk menyelesaikan permasalahan matematika secara efisien. Selanjutnya disini.