Dear Parents,
Apakah Anda dulu termasuk salah satu murid yang kesulitan dalam pelajaran matematika? Atau bahkan Anda menganggap bahwa matematika itu suatu hal yang menyeramkan? Jika ya, mungkin sekarang Anda memiliki rasa khawatir jika anak Anda merasakan hal yang sama dengan Anda semasa sekolah dulu.
Matematika bisa menjadi sesuatu yang menyeramkan bagi anak Anda jika mereka mengalami hal-hal berikut ini: Kesulitan dalam memahami soal saat ujian, Kebingungan dalam menentukan konsep yang harus dipakai, Membutuhkan waktu yang lama untuk menyelesaikan satu soal
Saat anak Anda mengalami hal-hal tersebut di sekolah, bukan tidak mungkin bagi mereka untuk meminta bantuan dari Anda di rumah. Oleh karena itu, memahami konsep matematika juga menjadi hal yang penting bagi Anda sebagai orang tua.
Melalui artikel ini, kami akan bagikan strategi math problem-solving untuk membantu Anda sebagai orang tua agar bisa memberikan pengawasan dan dukungan yang tepat bagi anak Anda agar bisa tumbuh menjadi anak yang cerdas.
Tiga langkah simple ini dapat membantu anak Anda dalam menyelesaikan soal-soal matematika. Yuk, simak apa saja poin-poin nya?

Anda perlu mengajari anak Anda untuk mengambil kata kunci di dalam setiap soal matematika khususnya pada soal cerita.
Kata kunci yang umumnya digunakan, antara lain:
Selain kata-kata yang tertera di atas, semua angka yang tertera pada soal juga merupakan kunci penting dalam menyelesaikan permasalahan soal. Setelah anak Anda mengidentifikasi setiap kata kunci, Anda harus memastikan apakah anak Anda sudah memahami betul maksud dari permasalahan soal yang diberikan.
Kami menyediakan latihan soal dengan petunjuk penyelesaiannya untuk melatih pemahaman anak Anda di sini.
Setelah memahami soal dan mendapatkan informasi penting, Anda kemudian perlu melatih anak Anda untuk menghubungkan informasi tersebut dengan konsep matematika yang tepat.
Misalnya,
Kata kunci “sisa” dapat dihubungkan dengan konsep percabangan (branching)
Kata kunci “lebih dari” atau “kurang dari” atau “2 kalinya” yang merupakan skenario sebelum dan setelahnya, dapat dihubungkan dengan gambar box model.
Soal bentuk pecahan yang melibatkan “ jumlah yang sama” dapat dihubungkan dengan konsep nilai pecahan setara dengan menyamakan pembilang.
Kata kunci “ pada akhirnya” dan “temukan nilai semula” dapat dihubungkan dengan konsep menghitung mundur/ terbalik (working backwards)
Soal yang berkaitan dengan “umur” dapat dihubungkan dengan selisih/ perbedaan nilai yang konstan atau tetap.
Soal yang berkaitan dengan “pemberian nilai” (internal transfer) dapat dihubungkan dengan konsep nilai total yang tetap atau konstan.
Agar anak Anda dapat dengan tepat menghubungkan antara informasi penting pada soal dengan konsep yang tepat digunakan, maka ia perlu memahami terlebih dahulu bagaimana cara kerjanya.
Misalnya, untuk “pemberian nilai” (internal transfer) soal, Anda dapat memberikan anak Anda sejumlah pensil dan Anda pun mendapatkan sejumlah pensil. Tanyalah kepada anak Anda berapakah total pensil (pensil Anda dan anak Anda) semula. Kemudian, berikan pensil Anda kepada anak Anda, dan tanyakan berapa total pensil di akhir. Pastinya total pensil semula dan di akhir akan bernilai sama, kecuali ada pensil yang patah atau hilang.
Setelah anak Anda mengambil kata kunci dan memahami soal dengan baik, kemudian mampu menghubungkannya dengan konsep matematika yang tepat digunakan, maka langkah selanjutnya adalah menerapkan konsep matematika tersebut.
Misalnya,
Pada konsep percabangan (branching), anak Anda perlu mengetahui kapan ia perlu mengalikan dan membagi suatu pecahan.
Pada konsep nilai pecahan setara, anak Anda perlu mengetahui bagaimana cara menjadikan nilai pembilang pada suatu bilangan pecahan menghasilkan nilai yang sama.
Pada konsep box model (dengan istilah kotak/ satuan/ bagian), anak Anda perlu mengetahui bagaimana menggunakan aljabar untuk menyelesaikan permasalahan soal yang sama baiknya dengan metode kali silang.
Setelah anak Anda menerapkan konsep matematika untuk menyelesaikan permasalah soal, pastikan bahwa anak Anda telah memeriksa jawabannya dengan mencocokkan kembali pada soal.
Ingatlah 3 langkah pendekatan ini dan gunakan untuk membantu melatih anak Anda. Dengan begitu, Anda akan dapat mengidentifikasi kelemahan anak Anda dan membimbingnya dengan baik.
Ketika anak bertanya tentang soal matematika, Anda tidak perlu langsung menjawab dengan bagaimana cara mengerjakannya. Ada cara yang lebih efektif, yaitu dengan memberikannya pertanyaan kembali yang bisa memberikan petunjuk untuk anak Anda. Pertanyaan dengan tujuan seperti ini disebut sebagai “Guiding Questions”.
Guiding questions ditujukan supaya anak Anda bisa memahami dan menghubungkan informasi-informasi yang ada pada soal. Selain itu, cara ini juga bisa membantu Anda untuk mengetahui apakah anak Anda sudah benar-benar mengerti soal yang sedang dihadapi atau tidak.
Ini dia beberapa contoh guiding questions yang bisa Anda gunakan:
Proses ini mungkin membutuhkan waktu yang lebih lama untuk membantu anak Anda menemukan jawabannya. Namun cara ini memungkinkan dia untuk dapat menjawab pertanyaan tersebut berkat dirinya sendiri dengan sedikit bantuan.
Dan ketika dia dapat menyelesaikannya sendiri, itu akan meningkatkan rasa percaya dirinya sehingga ia dapat menyelesaikan soal-soal lain yang mirip tanpa bantuan Anda.
Melalui tulisan ini, Anda akan mempelajari konsep-konsep penting untuk memecahkan berbagai jenis soal penjumlahan.
Membaca dan memahami contoh soal hanyalah setengahnya dari permasalahan soal penjumlahan yang perlu dikuasai. Anak Anda pun harus melakukan latihan.
Biasanya saat musim ujian, banyak orang tua yang menyuruh anaknya untuk mengerjakan soal-soal sebelumnya seperti soal tahun lalu. Padahal, mudah saja bagi anak untuk melihat solusi soal yang biasanya tertera di lembar paling belakang. Mayoritas anak melakukan itu ketika ia merasa pikirannya buntu.Sayangnya, solusi tersebut kurang spesifik dan melewati bagian terpenting dari sebuah penyelesaian soal matematika.
Dalam latihan, saya percaya bahwa sedikit mengerjakan itu lebih baik dibandingkan banyak mengerjakan tapi tidak efektif. Anak Anda tidak harus mengerjakan banyak latihan soal. Namun, ia perlu mengerjakan latihan soal yang tepat dan memastikan bahwa ia sudah sepenuhnya memahami tiap soal dan juga penyelesaiannya.
Bagaimanakah caranya? Berikut kami berikan petunjuk untuk membimbing anak Anda.
Kapanpun anak Anda mengerjakan latihan soal, mintalah kepada anak Anda untuk menuliskan konsep yang tepat digunakan untuk soal tersebut di sebelah soalnya.
Konsep itu berbeda dengan topik. Jangan menuliskan "pecahan", tapi tulislah "nilai pecahan setara".
Anda dapat membimbing anak Anda dengan menggunakan Guiding Questions sebelum anak Anda mengidentifikasi konsep yang tepat untuk digunakan.
Di akhir, jangan lupa untuk memeriksa solusi soal dan berilah tanda pada konsep yang kira-kira belum anak Anda pahami.
Kemudian berikan soal latihan lain dan pilih beberapa soal yang menggunakan konsep yang sama. Jika ingin lebih mudah, ganti saja angka pada soal sebelumnya dengan angka baru yang Anda buat dan biarkan anak Anda mengerjakan soal tersebut.
Pastikan anak Anda mengerjakan soal tersebut sampai ia merasa percaya diri untuk mengerjakannya secara mandiri. ingatlah jangan terburu-buru dalam mengerjakan, pastika ia mengerjakan dengan teliti dan sistematis, langkah demi langkah.
Walaupun hal tersebut membutuhkan waktu yang relatif lebih lama, namun hal tersebut akan memungkinkan bahwa anak anda bener-benar memahami alur penyelesaian soal tersebut dengan baik.
Lebih baik menghabiskan waktu 30 menit untuk 1 soal dan pastikan sudah memahami sepenuhnya, daripada menghabiskan 30 menit untuk 10 soal tapi hanya membaca dari hasil jawaban pada lembar belakang.
Contoh 1:
Vira memiliki sejumlah uang. Dia menggunakan 1/7 dari total uangnya untuk membeli baju dan 5/12 dari sisanya untuk membeli buku. Berapa nilai pecahan yang menggambarkan sisa uang Vira? Nyatakan dalam nilai pecahan paling sederhana.
Sisa uang Vira digambarkan dengan nilai ...
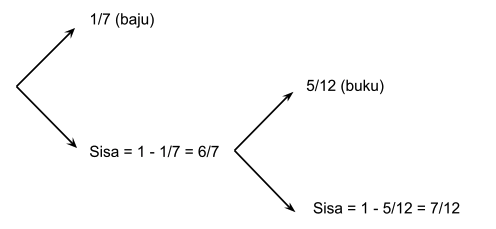
Sisa uang Vira = 6/7 x 7/12 = 42/84 = 1/2
Contoh 2 (lanjutan dari contoh 1):
Jika Vira memiliki sisa uang Rp 210.000, berapa jumlah uang Vira semula?
1 satuan = Rp 210.000
2 satuan = Rp 210.000 x 2 = Rp 420.000
Jadi, uang Vira semula adalah Rp 420.000
Catatan: jika anak Anda lemah pada konsep percabangan atau belum mempelajarinya, Anda dapat menggunakan box model untuk menjelaskan kepadanya. Meskipun begitu, saya merekomendasikan konsep percabangan untuk menyelesaikan soal “sisa” seperti ini untuk lebih mempersingkat waktu pengerjaan.
Langkah 1: gambarlah 7 buah kotak yang memiliki ukuran sama besar.

Langkah 2: tandai baju dan sisanya
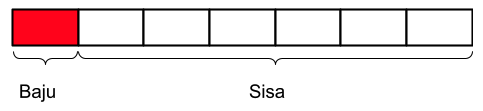
Langkah 3: bagilah tiap kotak menjadi 2 bagian
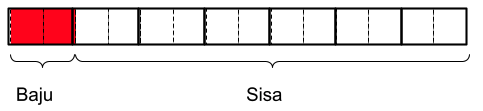
Langkah 4: tentukan banyaknya kotak atau satuan untuk menggambarkan buku dan sisanya.
Buku = 5/12 x 12 = 5 kotak
Sisanya = 12 - 5 = 7 kotak
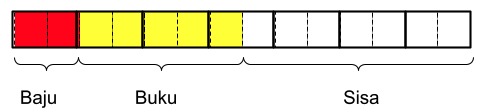
Langkah 5: tentukan nilai pecahan yang menggambarkan sisa di akhir
Jumlah sisa = 7/14 = 1/2
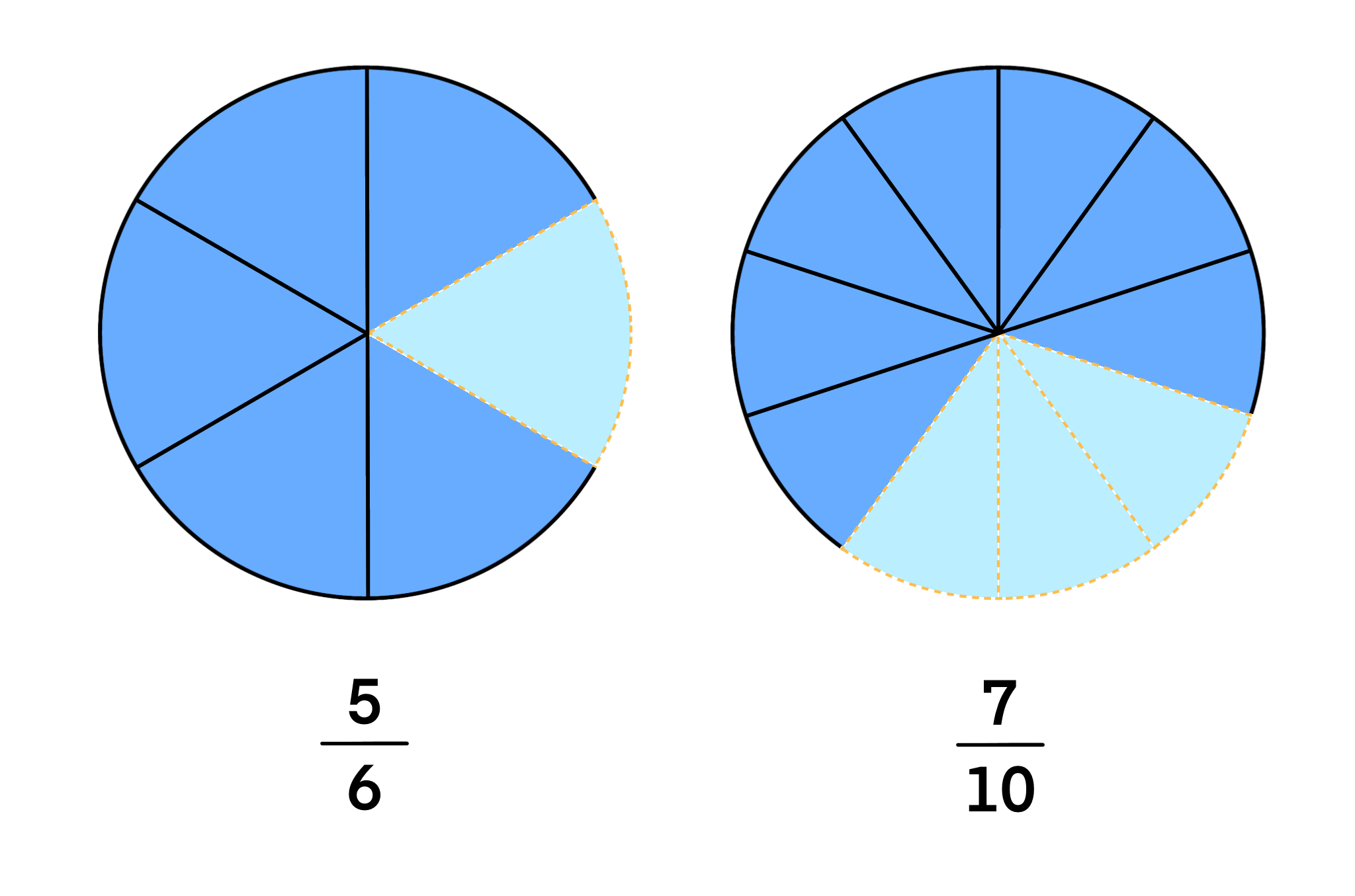
Ini adalah salah satu konsep umum yang paling sering membuat anak terjebak. Pada konsep ini, Anda perlu menjadikan pembilangnya bernilai sama (bukan penyebutnya)
Ketika disebutkan ⅞ dari jumlah laki-laki sama dengan ⅖ dari jumlah perempuan. Berapakah rasio/ perbandingan dari laki-laki dan perempuan?
Langkah 1: jadikan pembilangnya bernilai sama
7/8 = 14/16
2/5 = 14/35
Langkah 2: bandingkan penyebutnya
Laki-laki : Perempuan
16 : 35
Contoh 1
102 penumpang kereta berada di gerbong C. ⅞ dari jumlah penumpang laki-laki sama dengan ⅖ dari jumlah penumpang perempuan. Berapa selisih penumpang perempuan dan laki-laki ?
Langkah 1: jadikan pembilangnya bernilai sama
7/8 = 14/16
2/5 = 14/35
Langkah 2: bandingkan penyebutnya
Laki-laki : Perempuan
16 : 35
Langkah 3: tentukan total satuan
16 + 35 = 51 (total)
35 - 16 = 19 (selisih)
51 satuan = 102
1 satuan = 102 / 51 = 2
19 satuan = 2 x 19 = 38
Contoh 2
Chevira memiliki beberapa permen coklat. Ia memberikan 42 buah kepada Fika dan 1/5 sisanya kepada Yalma. Jika Chevira masih punya ½ nya permen coklat dari jumlah awal. Berapa banyak permen coklat Chevira mulanya?
Permen coklat Chevira mulanya ada …. buah.
Langkah 1: gunakan metode percabangan untuk menemukan sisa di akhir.
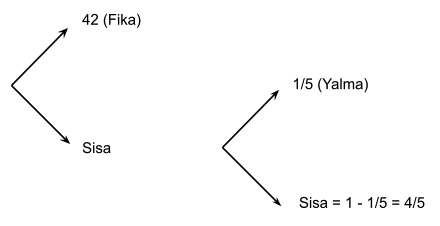
Langkah 2 : bandingkan sisa dengan total permen semula
⅘ dari sisa = ½ dari total
Langkah 3: jadikan pembilangnya bernilai sama
½ = 4/8
Langkah 4: bandingkan penyebutnya
Sisa : Total
5 : 8
Langkah 5: tentukan selisih dari sisa dan bagilah dengan jumlah permen yang diberikan kepada Fika
8 - 5 = 3 satuan
3 satuan = 42
Langkah 6: tentukan nilai 1 satuan
1 satuan = 42 ÷ 3 = 14
Langkah 7: tentukan jumlah permen semula
8 satuan = 14 x 8 = 112
Dengan memahami konsep matematika seperti yang telah dijelaskan di atas, anak akan merasa lebih mudah dan percaya diri dalam mengerjakan soal sesulit apapun. Pelajari konsep matematika lainnya di sini.